Slope Calculator
Compute slope, angle, and distance using points and slope
๐
Slope Calculator
Calculate slope (gradient), angle of incline, and distance. Enter two points or one point with slope (or angle) and distance.
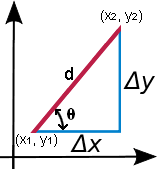
By definition, the slope or gradient of a line describes its steepness, incline, or grade.
Where
- m โ slope
- ฮธ โ angle of incline
m =
= tan(ฮธ)
| y2 โ y1 |
| x2 โ x1 |
Quick Navigation
๐งฎ If the 2 Points are Known
๐ Result
ฮX
1
ฮY
1
Slope (m)
1
Angle (ฮธ)
45ยฐ
Distance (d)
1.4142
Line equation
y = x
y-intercept (when x=0)
0
x-intercept (when y=0)
0
๐ If 1 Point and the Slope are Known
๐งพ Result
Given slope (m)
0.75
Angle (ฮธ)
36.87ยฐ
Xโ = 5
Yโ = 4
ฮX = 4
ฮY = 3
ฮธ = 36.869897645844ยฐ
Equation of the line:
y = 0.75x + 0.25
When x=0, y = 0.25
When y=0, x = -0.3333333333333333
OR
Xโ = -3
Yโ = -2
ฮX = -4
ฮY = -3
ฮธ = 216.869897645844ยฐ
Equation of the line:
y = 0.75x + 0.25
When x=0, y = 0.25
When y=0, x = -0.3333333333333333
Understanding Slope
Slope, sometimes referred to as gradient in mathematics, measures the steepness and direction of a line, usually denoted by m. The larger |m| is, the steeper the line.
- A line increases (upwards left-to-right) when m > 0
- A line decreases when m < 0
- A horizontal line has m = 0
- A vertical line has undefined slope
Slope is often described as "rise over run" and represented as m = (yโ โ yโ) / (xโ โ xโ) = tan(ฮธ). The distance between two points is computed using the Pythagorean theorem.
Formulas
m = (yโ โ yโ) / (xโ โ xโ)
ฮธ = arctan(m)
d = โ((xโ โ xโ)ยฒ + (yโ โ yโ)ยฒ)