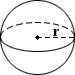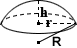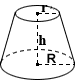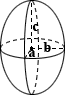Volume Calculator
Compute volumes for common 3D shapes with unit options
Volume Calculator
The following is a list of volume calculators for several common shapes. Please fill in the corresponding fields and click the "Calculate" button.
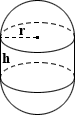
๐ขSphere Volume
Formula
volume = (4/3) ร ฯ ร r^3
Result
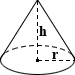
๐งCone Volume
Formula
volume = (1/3) ร ฯ ร r^2 ร h
Result
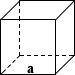
๐งCube Volume
Formula
volume = a^3
Result
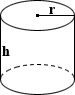
๐ข๏ธCylinder Volume
Formula
volume = ฯ ร r^2 ร h
Result
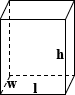
๐ฆRectangular Tank Volume
Formula
volume = length ร width ร height
Result
๐Capsule Volume
Formula
volume = ฯ ร r^2 ร h + (4/3) ร ฯ ร r^3 = ฯ ร r^2 ร (h + 4r/3)
Result
๐ขSpherical Cap Volume
Formula
volume = (1/3) ร ฯ ร h^2 ร (3R โ h)
Result
๐บConical Frustum Volume
Formula
volume = (1/3) ร ฯ ร h ร (r^2 + rR + R^2)
Result
๐ฅEllipsoid Volume
Formula
volume = (4/3) ร ฯ ร a ร b ร c
Result
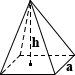
๐บSquare Pyramid Volume
Formula
volume = (1/3) ร a^2 ร h
Result
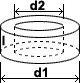
๐งชTube Volume
Formula
volume = ฯ ร (d1^2 โ d2^2) / 4 ร l
Result
Common Volume Units
| Unit | cubic meters | milliliters |
|---|---|---|
| milliliter (cubic centimeter) | 0.000001 | 1 |
| cubic inch | 0.00001639 | 16.39 |
| pint | 0.000473 | 473 |
| quart | 0.000946 | 946 |
| liter | 0.001 | 1,000 |
| gallon | 0.003785 | 3,785 |
| cubic foot | 0.028317 | 28,317 |
| cubic yard | 0.764555 | 764,555 |
| cubic meter | 1 | 1,000,000 |
| cubic kilometer | 1,000,000,000 | 10^15 |
About Volume and Shape Formulas
Volume is the quantification of the three-dimensional space a substance occupies. The SI unit for volume is the cubic meter, or m^3. By convention, the volume of a container is typically its capacity, and how much fluid it is able to hold, rather than the amount of space that the actual container displaces.
Volumes of many shapes can be calculated by using well-defined formulas. In some cases, more complicated shapes can be broken down into simpler aggregate shapes, and the sum of their volumes is used to determine total volume. The volumes of other even more complicated shapes can be calculated using integral calculus if a formula exists for the shape's boundary.
Alternatively, if the density of a substance is known, and is uniform, the volume can be calculated using its weight. This page provides calculators for some of the most common simple shapes and summarizes formulas and examples for each.